- (a)
- Definition of class Rectangle:
class Rectangle inherits from Point { attributes: int _width, // Width of rectangle _height // Height of rectangle methods: setWidth(int newWidth) getWidth() setHeight(int newHeight) getHeight() }In this example, we define a rectangle by its upper left corner (coordinates as inherited from Point) and its dimension. Alternatively, we could have defined it by its upper left and lower right corner.
We add access methods for the rectangle's width and height.
- (b)
- 3D objects. A sphere is defined by a center in 3D space and a
radius. The center is a point in 3D space, thus, we can define class
Sphere as:
class Sphere inherits from 3D-Point { attributes: int _radius; methods: setRadius(int newRadius) getRadius() }This is similar to the circle class for 2D space. Now, 3D-Point is just a Point with an additional dimension:
class 3D-Point inherits from Point { attributes: int _z; methods: setZ(int newZ); getZ(); }Consequently, 3D-Point and Point are related with a is-a relationship.
- (c)
- Functionality of move(). move() as defined in the
section allows 3D objects to move on the X-axis, thus only in one
dimension. It does this, by modifying only the 2D part of 3D objects.
This 2D part is defined by the Point class inherited directly or
indirectly by 3D objects.
- (d)
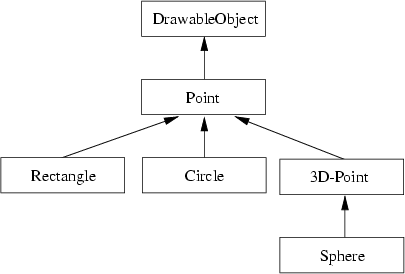
- Inheritance graph (see Figure A.1).
- (e)
- Alternative inheritance graph. In this example, class Sphere inherits from Circle and simply adds a third coordinate. This has the advantage that a sphere can be handled like a circle (for example, its radius can easily be modified by methods/functions which handle circles). It has the disadvantage, that it ``distributes'' the object's handle (the center point in 3D space) over the inheritance hierarchy: from Point over Circle to Sphere. Thus, this handle is not accessible as a whole.
However, these properties are uniquely identified by following the path from D up to A. Thus, D can change properties of A inherited by B by following the inheritance path through B. Similarly, D can change properties of A inheritied by C by following the inheritance path through C. Consequently, this naming conflict does not necessarily lead to an error, as long as the paths are designated.